Στοχαστική Αεροελαστικότητα και Πτερυγισμός

Στοχαστικές Διαδικασίες

Οι στοχαστικές διαδικασίες είναι μαθηματικά μοντέλα που χρησιμοποιούνται για να περιγράψουν τη συμπεριφορά τυχαίων μεταβλητών με την πάροδο του χρόνου. Στη μηχανική, οι στοχαστικές διαδικασίες χρησιμοποιούνται για τη μοντελοποίηση και ανάλυση συστημάτων που υπόκεινται σε αβεβαιότητα. Μαθηματικά, οι στοχαστικές διεργασίες μπορούν να αναπαρασταθούν με διάφορους τρόπους, συμπεριλαμβανομένων των Random Walks, της κίνησης Brown και των παραγώγων αυτής, ή ως λύσεις σε στοχαστικές διαφορικές εξισώσεις. Αυτά τα μοντέλα μπορούν να χρησιμοποιηθούν για τη δημιουργία τυχαίων ακολουθιών τιμών που αντιπροσωπεύουν τη εξέλιξη ενός συστήματος με την πάροδο του χρόνου.
Αναλύοντας αυτές τις ακολουθίες, οι μηχανικοί μπορούν να αποκτήσουν γνώσεις για τη συμπεριφορά ενός συστήματος κάτω από διαφορετικές συνθήκες λειτουργίας και να χρησιμοποιήσουν αυτές τις πληροφορίες για να βελτιστοποιήσουν την απόδοση και την αξιοπιστία του συστήματος αυτού. Παρέχοντας ένα ισχυρό εργαλείο για τη μοντελοποίηση και την ανάλυση της αβεβαιότητας, οι στοχαστικές διαδικασίες μπορούν να να επιτρέψουν στους μηχανικούς να σχεδιάσουν πιο αποδοτικές και αποτελεσματικές λύσεις σε ένα ευρύ φάσμα προβλημάτων μηχανικής.

Στοχαστική Αεροελαστικότητα

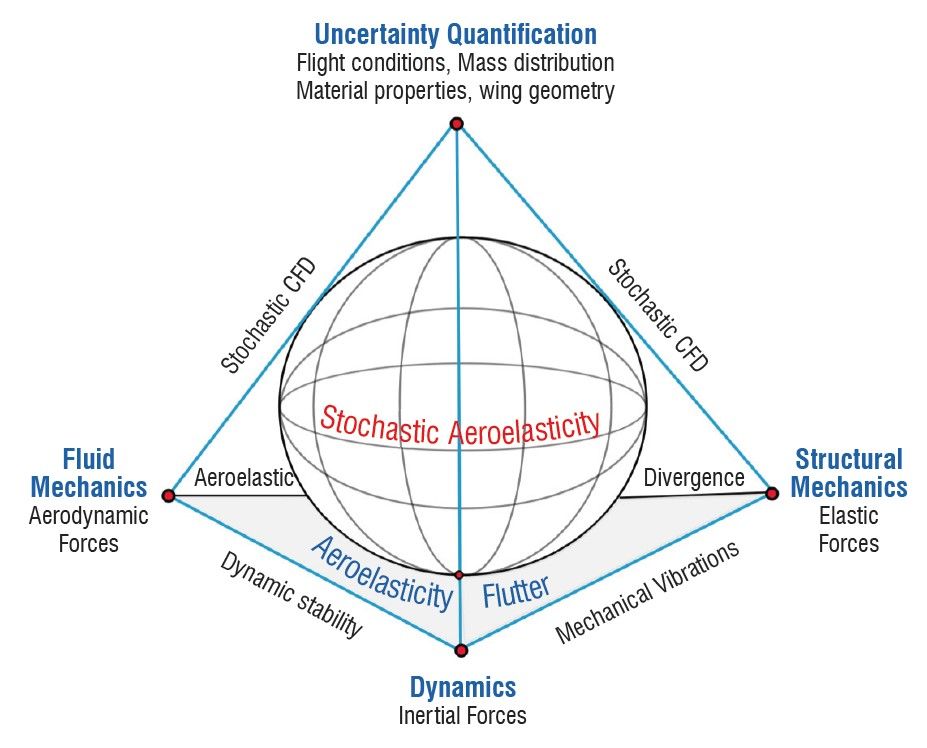
Η στοχαστική αεροελαστικότητα είναι η επέκταση της κλασικής αεροελαστικότητας που λαμβάνει υπόψη τις επιδράσεις της τυχαιότητας και των αβεβαιοτήτων (διακυμάνσεις μίας μη ιδανικής ροής, ριπές ανέμου, κατασκευαστικές ατέλειες) (βλ. Εικόνα 1). Είναι ένα σημαντικό πεδίο έρευνας στην αεροδιαστημική μηχανική, καθώς επιτρέπει την ανάλυση και τον σχεδιασμό αεροδιαστημικών κατασκευών υπό ρεαλιστικές συνθήκες λειτουργίας. Περιλαμβάνει τη χρήση των πιθανολογικών μοντέλων που αναφέρθηκαν από πάνω καθώς και μεθόδων για την ποσοτικοποίηση των αβεβαιοτήτων στα αεροδυναμικά φορτία και τη δομική απόκριση ενός εναέριου μέσου.

 

Εφαρμογές – Στοχαστική Μελέτη Πτερυγισμού

Όπως έχει αναφερθεί σε προηγούμενο άρθρο (Το Πρόβλημα του Πτερυγισμού (Wing Flutter): Πως, Γιατί και Πότε Εμφανίζεται;), ο Πτερυγισμός είναι μια αυτοδιεγούμενη αεροελαστική αστάθεια που μπορεί να συμβεί για παράδειγμα στα φτερά ενός αεροσκάφους. Είναι ένα δυνητικά καταστροφικό φαινόμενο που μπορεί να οδηγήσει σε δομική αστοχία κατασκευών και απώλεια ζωών. Η ανάλυση του στοχαστικού πτερυγισμού περιλαμβάνει τη χρήση στοχαστικών μοντέλων και μεθόδων για την ρεαλιστικότερη πρόβλεψη της πιθανότητας εμφάνισης πτερυγισμού και την εκτίμηση του κινδύνου δομικής αστοχίας. Η διαδικασία Ornstein – Uhlenbeck είναι μια ευρέως χρησιμοποιούμενη στοχαστική διαδικασία στην ανάλυση στοχαστικού πτερυγισμού (παράδειγμα βλ. Εικόνα 2). Βρίσκει ιδιαίτερη εφαρμογή στην προσημείωση της χρηματιστηριακής εξέλιξης της τιμής αγαθών στο χρηματιστήριο, αγαθών όπως ο χρυσός και το πετρέλαιο των οποίων η τιμή δεν εξελίσσεται ελευθέρα, αλλά περιορίζεται από μία διαχρονική μέση τιμή. Η διαδικασία OU μπορεί να χρησιμοποιηθεί με την κατάλληλη τροποποίηση των μεταβλητών της για τη μοντελοποίηση των τυχαίων διακυμάνσεων μίας ροής καθώς και των επιπτώσεων των αναταράξεων, που είναι μια κύρια πηγή αβεβαιότητας στην ανάλυση πτερυγισμού.

 

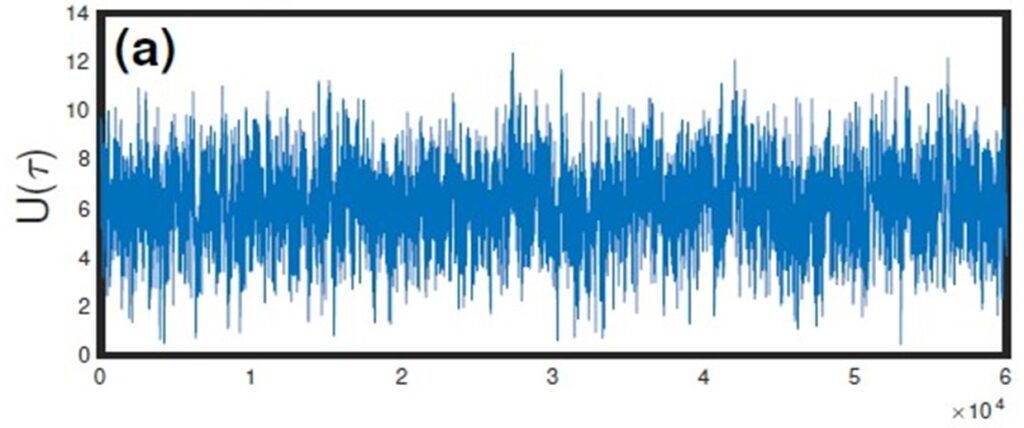
Η μελέτη του στοχαστικού πτερυγισμού έχει αρκετά πλεονεκτήματα σε σχέση με την κλασική ανάλυση πτερυγισμού. Πρώτον, επιτρέπει μια πιο ρεαλιστική αναπαράσταση των τυχαίων διακυμάνσεων στα αεροδυναμικά φορτία και της δομικής απόκρισης μίας πτέρυγας. Η κλασική ανάλυση πτερυγισμού προϋποθέτει ντετερμινιστικές ροές, οι οποίες μπορούν να οδηγήσουν σε υπερβολικά συντηρητικές προβλέψεις της συμπεριφοράς του Flutter. Η στοχαστική ανάλυση πτερυγισμού, από την άλλη πλευρά, λαμβάνει υπόψη τις επιπτώσεις της τυχαιότητας, παρέχοντας μια πιο ακριβή και αξιόπιστη πρόβλεψη της πιθανότητας εμφάνισης πτερυγισμού και του κινδύνου δομικής αστοχίας.

Μελλοντικές Εξελίξεις

Όπως οι κλασσικές, έτσι πλεόν και οι στοχαστικές αναλύσεις πτερυγισμού χρησιμοποιούνται στην αεροδιαστημική βιομηχανία, ανάλογα με τη φύση της υπό εξέτασης εφαρμογής και το επίπεδο ακρίβειας που απαιτείται. Για πολλές εφαρμογές, η κλασική ανάλυση πτερυγισμού είναι αρκετή για να παρέχει μια καλή εκτίμηση. Ωστόσο, για πιο σύνθετες εφαρμογές (υπερηχητικά αεροσκάφη, εμπορικά αεροσκάφη με νέα σχέδια πτερυγίων, UAVs που πετούν κοντά σε απρόβλεπτα περιβάλλοντα όπως βουνοπλαγιές και θάλασσες), η στοχαστική ανάλυση προτιμάται συχνά. Τα τελευταία χρόνια, υπάρχει αυξανόμενο ενδιαφέρον στην αεροδιαστημική βιομηχανία να ενσωματώσει μεθόδους στοχαστικής ανάλυσης στη διαδικασία σχεδιασμού ενός αεροσκάφους, καθώς αυτές προσφέρουν μια πιο ρεαλιστική και ακριβή αναπαράσταση της συμπεριφοράς πολύπλοκων φαινομένων υπό αβέβαιες συνθήκες λειτουργίας. Πολλές εταιρείες αεροδιαστημικής επενδύουν στην έρευνα και ανάπτυξη, για να προωθήσουν τις δυνατότητες των εργαλείων στοχαστικής ανάλυσης και να βελτιώσουν την ακρίβεια και την αποτελεσματικότητά τους. Ως αποτέλεσμα, αναμένεται η χρήση της στοχαστικής ανάλυσης πτερυγισμού να γίνει ακόμα πιο διαδεδομένη στην αεροδιαστημική βιομηχανία στο μέλλον, ειδικά καθώς η ζήτηση για πιο σύνθετα και προηγμένα αεροσκάφη συνεχίζει να αυξάνεται, όπως έχει αναφερθεί και στο άρθρο Η Επάνοδος των Υπερηχητικών Επιβατικών Αεροσκαφών (Supersonic Transport): Η Νέα Γενιά.

Βιβλιογραφία

D. Ketseas, (2022), Δυναμική συμπεριφορά αεροτομής σε εξαναγκασμένη και ελεύθερη ταλάντωση. Επίλυση του αεροελαστικού προβλήματος σε περιβάλλον ANSYS FLUENT
D. Ketseas, (2019), Διαδικασίες Ornstein-Uhlenbeck και εφαρμογές τους
J. Chassaing, C. Nitschke, A. Vincenti, P. Cinnella, D. Lucor, (2018), Advances in Parametric and Model-Form Uncertainty Quantification in Canonical Aeroelastic Systems, Engineering
H. Varun, M. Aswathy, S. Sarkar, (2020), Stochastic resonance in a parametrically perturbed aeroelastic system, ENOC
D. S. Lemons, (2002), An Introduction to Stochastic Processes in Physics
A. K. Dixit, R. S. Pindyck, (1994), Investment under Uncertainty